Matematikailag bizonyított, hogy a prímszámok száma végtelen. Ez azért jó hír, mert ez azt jelenti, hogy az RSA eljárásban használt prímek hosszát, azaz a titkosítás erősségét tetszőlegesen lehet növelni. A kérdés csupán az: hogyan döntsük el egy több, mint száz jegyű számról, hogy prím-e. Az RSA eljárás alapja, hogy nagyon nagy szám faktorizálása sokáig tart. A véletlenszerűen választott prímről eldönteni, hogy valóban prím-e, éppen ezért pontosan ugyanolyan nehéz feladat, mint az eljárással titkosított üzenetet brute force módszerrel feltörni. Másképp: ha létezne gyors módszer arra, hogy egy nagy számot gyorsan faktorizálni tudjunk, akkor minden, RSA-val titkosított üzenet könnyen megfejthetővé válna.
Más módszert kell tehát találni, hogy egy szám prím mivoltát ellenőrizni tudjuk. Ilyen módszerek léteznek: valószínűségi prímtesztek. Ezek az eljárások nem 100%-os biztonsággal mondják meg, hogy egy szám prím-e, hanem csak valamekkora valószínűséggel, ám a teszt többszöri lefuttatásával a tévedés valószínűsége tetszőlegesen kicsire csökkenthető. A gyakorlatban 0,99...9 (15 db 9-es számjegy) valószínűséget várnak el, hogy a választott szám prím legyen. Vagyis mindössze 10-16 a valószínűsége annak, hogy tévedünk, azaz a szám, amiről azt gondoljuk, hogy prím, valójában mégsem prím. Egy ilyen módszer Fermat tétele, vagy a Fermat-teszt:
Ha p prímszám, mely nem osztója egy a egésznek, akkor ap-1-1 osztható p-vel.
Ugyanakkor az állítás megfordítása nem feltétlenül igaz, holott a Fermat-teszt pont a megfordításra épül. Ezért az összefüggés néha bizonyos a számokra igaz még akkor is, ha p nem prím, azaz a teszt téved. Azonban ezeket az a-kat ki lehet szűrni. További valószínűségi prímtesztek a Solovay-Strassen és Miller-Rabin tesztek.A determinisztikus prímteszt 100% biztonsággal megállapítja egy számról, hogy prím vagy sem. Ám ez egy exponenciálisan lassú algoritmus, így nagy számokra nem alkalmazható. Számítógéptől függően (egy kb. 1 GHz-es processzorral felszerelt gép) 16 jegyű számot még pillanatok alatt faktorizál, ám minden egyes újabb számjegy esetén 10-szer annyi időre van szükség.
Prímek eloszlása
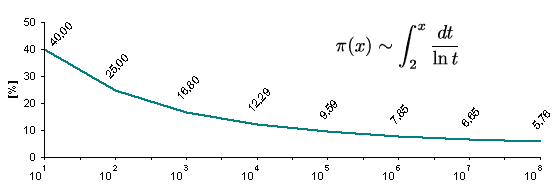
Ha fix hosszú, például 155 jegyű prímet keresünk (az RSA-155 eljárás 155 decimális jegyű, 512 bites prímeket használ), akkor azt egy közel 10155 hosszú intervallumban tehetjük meg. Azonban a prímek eloszlása, Gauss képlete szerint nem lineáris: Pi(x) jelöli a prímek számát a [0; x] intervallumban.

Az ábráról leolvashatjuk, a [0; x] intervallumnak hány százaléka prím. Látható, hogy az előfordulás valószínűsége az x intervallumhatár (exponenciális) kitolásával egyre csökken. Ez azt is jelenti, hogy a prímek közötti távolságok egyre nőnek. Ez megnehezíti a keresést, de megnehezíti a támadást is.
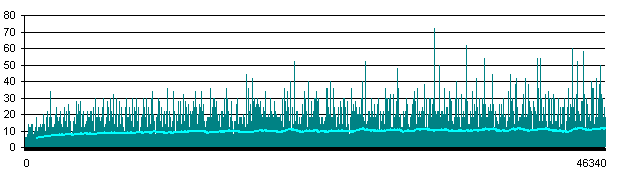
Az ábrán megfigyelhető, hogy a [0; 46340] intervallumban két szomszédos prím között mekkora a távolság, azaz a két prím között mennyi nem-prím található. A legnagyobb "hézag" 31397 és 31469 van: ez egy 72 hosszú intervallum, ahol nincs prím. Másképpen megfogalmazva: a [0; 46340] intervallumnak bármely, 72-nél hosszabb részintervallumában biztosan van legalább egy prím. Ám mivel az eljáráshoz két prímre van szükség, ezért nem elég a leghosszabb hézagra minimalizálni a keresési intervallumot, hanem az előtte/utána következő hézagok közül a hosszabbikat is hozzá kell venni. Ez esetünkben 4 és 8. Így jön ki a 72 + 8 = 80 minimális intervallumhossz.
A világosabb színű vonal az átlagos hézaghossz 100-hosszú intervallumonként. Látható, hogy a görbe erőteljes hullámzása mellett is emelkedő jelleget mutat, azaz minél nagyobb számokból álló fix hosszú intervallumban keresünk, annál kisebb a valószínűsége, hogy ott prímet találunk. Másképp: ha szűk intervallumban keresünk, kevesebb prím közül választhatunk, s ezt egy támadó ki tudja használni brute force módszerének finomítására.
Matematikailag bizonyított, hogy a prímszámok között tetszőleges nagy hézagok vannak. Ugyanakkor a Csebisev-tétel szerint minden természetes szám és kétszerese között van prímszám.
Mersenne-prímek
Nem szorosan ide kapcsolódik, inkább csak érdekesség: számos képlet létezik, amely segítségével prímet lehet előállítani. Ezek a képletek azonban nem tökéletesek, sokszor téves eredményt produkálnak, ezért a generált számot mindig ellenőrizni kell.
A Mersenne-prímeket az alábbi képlet állítja elő:
Mp = 2p - 1
Az interneten ma is folyik a Mersenne-prímek keresése: The Great Internet Mersenne Prime Search. A legújabb eredmény 2003. november 17-én született meg: a 40. Mersenne-prím, 220996011 - 1 pontosan 6320430 számjegyű.